「あ、春田くんじゃない」
振り返るとそこには長い黒髪の女性が立っていた。清水さんだ。彼女は僕の大学の同級生で、1年生のときの語学のクラスでいっしょだった。とても知性的でクールな雰囲気だが、ときどきみせるおっちょこちょいなところが親しみを感じさせる。この春2年生になってからは話す機会が減っていた。
「やあ、久しぶり。どうして鴨川デルタに?」
鴨川デルタというのは京都にある、高野川と加茂川の合流地点にある川に挟まれた逆三角形の形をした公園のことである。
「ちょうど今の時間空きコマで、鴨川の桜並木を見に来たの。春田くんもこの時間空きコマなの?」
「僕は一応3年生配当の量子力学の授業があるよ。でもあの範囲、以前自分で勉強したことがあるから、授業は受けなくていいかなと思ってる。テストだけ受けて単位をとるつもり。それでせっかくいい天気だし、川でも眺めながらのんびり本でも読もうと思って。」
僕は物理学に興味があり、将来は研究者になりたいと思っている。いつも土日は図書館が開くと同時に入館し、膨大な図書の中からいくつか気になった本を手に取り、閉館時までゆったり読むという生活をしている。それで先週閉館間際に書庫でふと手にとったのがランダウという人の本だった。埃を払い落として中身をパラパラと開いてみると、堅い文体の中に何やら厳めしい数式が並んでいる。軽く何ページか読み流してみたところ、その本には、もはや哲学とでも呼べるような、著者の深い物理的考察が隅々にあらわれていることが感じられた。これは良い本に出会ったと思った僕は借りることにし、それ以来いつもどこへ行くにしてもカバンに入れるようにしている。
「そうなのね。春田くんらしいね。」
そう言いながら清水さんは僕の傍らに腰を下ろした。それからはたわいもないことを話していた。サークルのこと、バイトのこと…。話が途切れ、少しして清水さんが「そういえば」と言い出した。
「そういえば鴨川デルタってどっちかといえば鴨川ナブラだよね?ナブラなんていう記号、ベクトル解析の授業を受けてはじめて知ったけど。」
「確かに地図上で見たら逆三角形だもんね。」
「記号は知ってるけどあんまりよくわかってないわ。ベクトル解析、あんまりよくわかんなくて…。春田くんはわかってるの?お願い教えて?」
「じゃあまずgradから説明しようか。スカラー場があるとするじゃん?」
「ねえスカラー場って何?あ、あれのこと?教授の出した論文の引用件数をこっそり調べちゃうゆつ。」
「グーグルスカラーのスカラーはscholarで学者とかの意味。今話しているのはscalarで、使われる文脈によっても変わってくるけど、今は実数くらいの意味だ。」
「どうしてただの実数にスカラーってわざわざ名付けるの?」
「ベクトルと対比させているからだよ。スカラー場っていうのはこんな感じで空間の各点各点がそれぞれ値を持っている。温度みたいなものだ。温度だって空間の各点各点で違う値を持っている。例えば上空では寒い。」
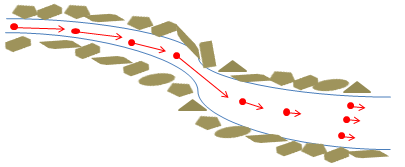
「でもこんなの高校の時とか大学1年生のときの数学の授業でも出てきたよね。\(f(x,y)=x^2+y^2\)とかもそうだよね。xy平面で各点各点が\(x^2+y^2\)という値を持っている。じゃあなんで今はこんな風にわざわざスカラーって名前を付けているかというと各点各点でベクトルが定義されたベクトル場がベクトル解析ではよく出てくるから、それと区別している。各点各点でベクトルが定義されるっていうと今までの数学的な概念として扱うのははじめてだけど、身近な例で考えるとありふれている。ほらあの鴨川の水の流れだってそうだよ。各時間ごとに水分子は速度を持っているよね。だから川の流れも各点ごとに速度が”埋め込まれている”ベクトル場だとみなすことができる。何点か空間の点をとってきて、そこに埋め込まれているベクトルを図示するとこんな感じになる。

もっと目に見えてわかりやすい例がある。たとえば中学校で磁石の周りに砂鉄をいっぱいおいたことなかった?そうするとこんなかんじになったよね?」

「砂鉄は磁石の磁界に沿って並ぶ性質があるから、砂鉄を置いた時のこの模様は磁界をあらわしているんだよね。これを見てわかる通り、磁界もベクトル場だ。磁石はその周りに、各点各点で、砂鉄をある方向に配列させてしまう力を生み出していることがわかる。磁力線だ。」
「スカラー場とベクトル場はわかったわ。でもgradってどういう意味なの?」
「gradは英語で勾配を意味するgradientの略だ。勾配といえば微分をイメージするよね。1変数関数ではまさにそのgradというのは微分係数のことだ。でも、例えば空気の気温というスカラー関数だって、変数は空間次元の数、つまり3つある(x,y,z)。ここの、陽だまりになっている場所と、あそこの桜の木陰では気温は少し違しね。そんな、関数が変数を複数持つ(多変数関数)場合にも勾配を考えたい場面はたくさんでてくる。そこで、微分係数という概念を、変数が複数ある場合にも拡張したものがgradという概念だ。」
「さあ、具体的に説明していこう。基本的な考えかたは変数がxだけの1変数関数f(x)での微分と同じだ。f(x)の微分を考えるときどうしたか覚えてる?」
(\(x_0\)での微分を考えたかったら、\((x_0,f(x_0)\)と、そこから曲線に沿って少しずれた点\((x_0+dx,f(x+dx))\)との傾きを求めればいいよね。数式で書けばこんな感じ。」
\(\frac{df}{dx}=\lim _{dx \rightarrow 0} \frac{f(x_0+dx)-f(x_0)}{dx}\)
「絵で描けばこうやってどんどん近づけていくイメージだよね。」

「そうだね。その精神で同じように考えれば多変数の微分も考えることができる。」
\(z=f(x,y)\)としてその関数形を表示しよう。そして、ある点\((x_0,y_0)\)(A点)を考えて、すこしずらした点\((x+dx,y+dy)\)(D点)との、zの差\(df=f_D-f_A\)を考えよう。

「今度は曲線じゃなくて曲面を近似するから、線じゃなくて四角形を考えるのね。こうやってその差を\(dx,dy\)で表そうというわけ?」
「その通り。x方向とy方向に分けて考えればすぐに求まる。分けるってことは偏微分を考えるんだね。」

「絵に示した通りに\(df\)を求めればいい。」
$$d f=f_{ D }-f_{ A }=(f_{ D }-f_{ B })+(f_{ B }-f_{ A })=\left. \frac{\partial f}{\partial x}\right|_{(x,y)=(x_0,y_0)} d x+\left. \frac{\partial f}{\partial y} \right|_{(x,y)=(x_0,y_0)}d y $$
「確かに\(f_B\)と\(f_A\)の差が\(\left. \frac{\partial f}{\partial x}\right|_{(x,y)=(x_0,y_0)} d x\)で書かれるのはわかるわ。でも少し気になるのは、どうして\(f_D\)と\(f_B\)の差が\(\left. \frac{\partial f}{\partial y} \right|_{(x,y)=(x_0,y_0)}\)で書かれるのかしら?厳密にはBやDのxの値って\(x_0\)じゃなくて\(x_0+dx\)だよね?」
「たしかにそうだね。でも\(dx\)はとても小さいから無視してもかまわない。もう少し正確に言うと、その変化は2次の微小量だ。\(\left. \frac{\partial f}{\partial y} \right|_{(x,y)=(x_0,y_0)}dy\)と\(\left. \frac{\partial f}{\partial y} \right|_{(x,y)=(x_0+dx,y_0)}dy\)の差はdxdy程度であって、微分をするときの極限の操作で消える量だ。この辺りは1変数のときに\(dx^2\)は無視した理由と同じだ。曲面を平面で近似しようとするときにはこういった2次の量は効いてこない。」
「なるほどね。じゃあ言ってたgradというのはどういうものかしら?」
「ここで2次元の勾配\(\rm{grad} f\)というのを\(\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)\)として定義しよう。このベクトルを使うと、さっきの\(df\)を変形して内積の形に表すことができる。」
\(df=grad f \cdot (dx,dy)\)
1変数の場合との対応表をこうやって作ると、gradが微分係数の拡張だっていうことがよりはっきりするね。

「gradについてその意味をもう少し詳しく見ていこう」
「1次元の場合は微分係数はスカラーで表された。2次元の場合、勾配は方向によってくる。具体例で考えてみよう。例えば先ほど挙げた\(f(x,y)=x^2+y^2\)を絵にするとこうなる。これは\(f(x,y)=x^2\)を回転させたものだ。だって極座標で書くと\(f(x,y)=r^2\)ってなるからね。ここで赤い点(\(x,y)=(1,1)\)での勾配を考えてみよう。」

「dx=dyとなる方向に進めば急だけどdx=-dyとなる方向なら高さが変わらないからその方向には勾配は0だ。ここで、方向による勾配の情報を含んでいるのがgradだ。まず、この場合にgradを求めてみる。」
\(\left. grad f=\left(\frac{\partial}{\partial x}(x^2+y^2),\frac{\partial}{\partial y}(x^2+y^2)\right)\right|_{(x,y)=(1,1)}=(2,2)\)
gradの決めかたから、関数の変化は\(grad f \cdot (dx,dy)\)で表されるんだった。
実際、\((dx:dy)=(1:1)\)の方向の場合なら勾配はたしかに\(\rm{grad} f \cdot (1,1)dx=4dx\)で急そうだし、\((dx:dy)=(1,-1)\)の方向の場合なら\(\rm{grad} f \cdot (1,-1)dx=0\)だ。」
「確かに、gradには注目している点での傾きが入っていることがわかるわね。」
gradの性質についてもうすこし考えてみよう。重要な性質として、grad fで表されるベクトルは一番関数fが変化しやすい方向を表している。これは別の言い方もできる。grad fは等高線と垂直な方向だ。さっきの例で等高線と\((1,1)\)での勾配ベクトルを図示するとこんな感じになる。

「たしかに勾配ベクトルの(2,2)は等高線と直交しているね。でもどうしてなの?」
「さっきのgrad \(f\)の決め方にもどればすぐにわかるよ。一般に勾配ベクトルが(a,b)のときにどの方向が最も勾配がきついか考えてみよう。つまり、\(adx+bdy\)が最も大きくなるような\((dx,dy)\)を考えればいい。その方向を\(\theta\)として\((dx,dy)=(\rm{cos} \theta,\rm{sin} \theta)\)とする。極座標で適当な\(r,\phi\)を用いて\((a,b)=r(\rm{cos} \phi,\rm{sin} \phi)\)とすると、
\(adx+bdy=r(\rm{cos} \phi \rm{cos} \theta+\rm{sin} \phi \rm{sin} \theta)=r\rm{cos} (\phi-\theta)\)
つまり\(\phi=\theta\)のとき最も勾配が大きくなって、その大きさはr、つまり\(\sqrt{a^2+b^2}\)であることがわかる。」
「gradを2変数の場合に説明したけど、これを3次元に拡張することもできる。単純に
\(\rm{grad} f=\left( \frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z} \right )\)
とすればいい。」
「物理学における応用例についても少し紹介しておこう。電場と電位との関係はgradを用いて書くことができる。\(E=-grad V(x)\)だ。高校のときに一様な電場があるときのコンデンサーでの電場と電位の関係E=V/dはこの式の特殊な場合に相当する。言い換えれば、このE=-gradVという式は、電場は電位の勾配だっていう概念を、電場が一様じゃない場合への一般化だ。厳密にはコンデンサーの電場だって一様ではない。コンデンサーの端っこでは電場は外側に向かっている。そんなときE=V/dという式はもはや適用できないから、高校の範囲では求めようがなかったわけだけど、このE=-gradVを使えば計算することは可能だ。」
(続く)


コメント